Определение площади плоских криволинейных структур произвольной конфигурации
Определение площади плоских криволинейных структур произвольной конфигурации (практические рекомендации)
Существует множество методов определения площади плоских криволинейных фигур, главным образом криволинейных трапеций. Методы довольно сложны и малопригодны для практического применения. Предложенный метод сравнительно прост и в тоже время достаточно точен.
Любая плоская фигура, образованная прямыми линиями, может быть преобразована в комбинацию из известных геометрических фигур типа треугольника, прямоугольника, квадрата, трапеции. Тогда её площадь определится как сумма площадей этих фигур по известным геометрическим формулам. Аналогичным способом можно преобразовать любую плоскую криволинейную фигуру произвольной конфигурации, вписав её в многоугольник, либо описав его. Однако, в таком случае образуются сегменты, состоящие из прямолинейного участка и кривой линии (рис1).

Рис 1 Плоская криволинейная фигура произвольной конфигурации, вписанная в многоугольник
Площадь многоугольника можно определить, разделив его на треугольники, площадь которых вычисляется по известным формулам, например по формуле:
Sтреуг. = [p(p - a) + p(p - b) + p(p - c)]0.5
Здесь p полупериметр треугольника, a, b и c – длины его сторон.
Площадь криволинейной фигуры, вписанной в многоугольник, определиться как разность площади многоугольника и сумме площадей криволинейных сегментов.
Площадь криволинейного сегмента можно определить, описав кривую уравнениями вида:
y = ax2 – bx ………………………………………………………… (1),
y = bx - ax2 ………………………………………………………… (1-a),
y = ax3 – bx2 …..…………………………………………………… (2),
y = bx2 - ax3 …,,,,,…………………………………………………… (2-a),
y = ax4 – bx3 …,,…………………………………………………… (3),
y = bx3 - ax4 …,,,,,,…………………………………………………… (3-a),
и т.д., или в общем виде:
y = axn – bxn-1 …,,,………………………………………………… (4).
y = bxn-1 - axn …,,,………………………………………………… (4-a).
Уравнения (1, (1-a)) описывают симметричный криволинейный сегмент, все другие уравнения описывают несимметричный криволинейный сегмент. Уравнения (1 - 4) описывают криволинейный сегмент с вершиной, расположенной ниже оси абсцисс, равнения (1а – 4а) описывают криволинейный сегмент с вершиной, расположенной выше оси абсцисс. Площадь криволинейного сегмента S определяется интегрированием из уравнения:
S = ʃ (axn – bxn-1)dx. S = ʃ (bxn-1 - axn)dx.
Интегрируя первое уравнение, получаем:
S = a * [1/(n+1)] * xn+1 – b * (1/n) * xn ……………………. (5).
Уравнения (1-4), описывающее криволинейный сегмент, имеют нулевое значение в его начале при x = 0 и в конце сегмента:
y = xn-1 (ax – b) = 0. ax – b = 0. ax = b, отсюда
x = b/a = l. Здесь l длина криволинейного сегмента, ордината которого в начале и конце равна 0.
Покажем на примере y = ax2 – bx как определить площадь криволинейного сегмента.
y = ax2 – bx; y = x (ax – b); При x1 = 0 y = 0 это – начальный участок криволинейного сегмента. С другой стороны y = 0, когда ax – b = 0. Тогда ax = b и x2 = = l. x2 = b/a = l. При любом значении показателя степени уравнений типа (1- 4) длина криволинейного сегмента равна отношению параметров b и a.
Дифференцируем уравнение (1):
yꞋ = 2ax – b. При yꞋ = 0 функция имеет экстремум.
Тогда: 2ax = b. При этом x, а это расстояние от начала координат (начало криволинейного участка), имеет значение: x = ½ ; x = ½ b/a = ½ l.;
Если криволинейный сегмент симметричен, то вершина криволинейного сегмента от его начала находится на расстоянии половины его длины x = ½ l. Высота h криволинейного сегмента определяется из уравнения:
y = a* [½ b/a]2 - b * [½ b/a]
y = a* [½l2] - b*[½l];
y = ½l * [½l * a - b ]; так как l * a = b, то
y = ½ l * [½b - b ];
y = ½ l * [- ½b ]; y = - 1/4lb
или: y = - 1/4 * l * a; y = - 1/4 * l 2* a.
В общем виде высота криволинейного сегмента:
h = {[(n - 1)(n – 1 )] / nn } * [ (a*l n) ] …………………. (6).
h = {[(n - 1)(n – 1 )] / nn } * [ (b *l n-1) ] ………………. (7).
Здесь n – показатель степени уравнения криволинейного сегмента, определяющий его форму (вид).
Параметры a и b уравнения криволинейного сегмента можно определить следующим образом:
Из уравнений (6) и (7 получаем:
a = [(nn / (n-1)(n-1)] * [(h / l n ] ………………………. (8).
b = [(nn / (n-1)(n-1)] * [(h / l n-1 ] …………………………. (9).
Тогда переписываем уравнение (5) в виде:
S = [a/n+1] * ln+1 – [b /n] * ln
Далее проводим преобразования:
S = ln [a/n+1] * l – [b /n] * ln;
S = ln [ (a/n+1) * l – (b /n)];
Так как b = a * l, то
S = ln [ (b/(n+1) – (b /n)];
S = ln { [ (bn - bn - b) / [ n * (n+1)] };
S = [b * ln ] / [ n* (n+1)];
В последнее уравнение подставляем выражение для b тогда при:
S = {n(n-1) / [ (n-1)(n-1) * (n+1) ] } * h l. …………………. (10).
Обозначим первые два члена полученного уравнения как коэффициент формы (вида) уравнения - Kf.
Kf = [1/(n+1)] * [n/(n-1)]]n-1 ………………………. (11).
тогда
S = Kf* h*l. ………………………. (12).
При n = 1 Kf = ½, криволинейное уравнение превращается в уравнение прямой, а формула площади становится площадью треугольника.
При n = 2 Kf = 2/3 (0,666..6); при n = 3 Kf = 9/16 (0,5625) и т.д. При n стремящемся к бесконечности Kf приближается к нулю, и площадь криволинейного сегмента также стремится к нулю.
Полученное уравнение можно использовать для определения площадей лесных пожаров, нефтяных разливов в море и на суше, для вычисления объёмов грунтов, потребных при возведении насыпей на болотах и переувлажнённых глинистых грунтах, в швейном деле и пр.
Покажем на примере возможность применения предложенного метода для вычисления объёмов земляных работ при возведении насыпей на болотах.
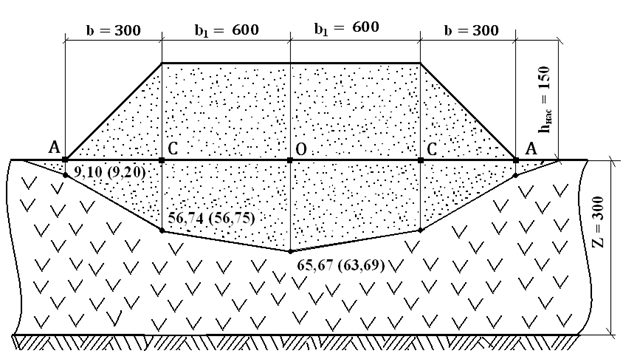
Рис 2 Поперечный профиль земляного полотна на болоте с использованием торфа в основании насыпи (размеры указаны в см)
На рис.2 показана кривая консолидации основания насыпи с указанием величины осадки насыпи в поперечном сечении, вычисленной согласно формулам механики грунтов. Посмотрим, насколько предлагаемые формулы совпадают с кривой консолидации. Поскольку осадка основания насыпи в большинстве случаев симметрична относительно её оси, в расчётах используем формулу 1: y = ax2 – bx. Определяем параметры уравнения а и в. Исходные данные: n = 2 h = 0,6567м l = 20м.
b = 4 * (0,6567 / 20) = 0,13134
b = a * l a = 0,13134 / 20/= 0,006567
Используя уравнение y = ax2 – bx, вычисляем значения y в точках А, С и О и сравниваем полученные значения с осадкой насыпи, вычисленные ранее по известным формулам механики грунтов.
в точке А: y = 0,006567 * 12 - 0,13134* 1 = - 0,124773 м. ( факт. 9,1 см.)
в точке С: y = 0,006567 * 42 - 0,13134* 4 = 0,10572 – 0,52536 = - 0,41788 м. ( факт. 56,74 см.)
в точке О: y = 0,006567 * 102 - 0,13134*10 = 0,6567 – 1,3134 = -0,6567 м. (факт. 65,67 см.)
Расчёты показали адекватность предложенного аналитического метода определения площади плоских криволинейных фигур для расчётов земляных работ при возведении насыпей на болотах. Для других случаев требуется дополнительная верификация.
Второй способ определения параметров математической кривой возможно получить воспользовавшись уравнениями типа:
y = axα – bxβ, y = bxβ - axα. Параметры уравнения a, α, b, β можно определить аналитико-эмпирическим методом.
Вышеприведённые уравнения, описывающее криволинейный сегмент, имеют нулевое значение в его начале при x = 0 и в конце сегмента:
При y = axα – bxβ = 0. axα – bxβ = 0. axα = bxβ, отсюда
(axα)/( bxβ ) = 1
(a/b) xα-β = 1
xα-β = b/a
логарифмируем последнее уравнение:
(α – β) lnx = lnb - lna.
lnx = (lnb - lna)/(α – β )
отсюда
x = e(lnb – lna)/( α-β )
Обозначим как ψ . Тогда x = eψ.
При таком значении x (на другом конце криволинейного сегмента) y = 0, а сама величина x определяет длину такого сегмента l. Тогда длина криволинейного сегмента:
l = eψ . l = e(lnb – lna)/( α-β )
Достове рность вычислений можно проверить контрольными формулами.
y = axα – bxβ, На конце криволинейного сегмента) y = 0, поэтому правильность вычисления и параметры можно проверить.
y = aeαψ - beβψ
Поскольку y = 0 aeαψ = beβψ ,
aeαψ/beβψ = 1,
(a/b) eα ψ -βψ = 1 eαψ - βψ = 1,
eα ψ -βψ = b/a
Подставляем в вышеприведённые формулы значения параметров, тем самым контролируем правильность вычислений.
Другой контрольной точкой является экстремум функции y = axα – bxβ. Дифференцируем вышеприведённое уравнение:
yꞋ = aαxα-1 – bβxβ-1. При yꞋ = 0 aαxα-1 = bβxβ-1.
aαxα-1 / bβxβ- 1= 1 .
(aα/bβ)*xα-β=1.
xα-β= bβ/aα.
Здесь x расстояние от начала криволинейного участка до экстремума.
x = [bβ/aα]1/(α-β)
Логарифмируем:
lnx = [1/(α – β)]* [ln (bβ) – ln (aα)]
lnx=[ln(bβ)–ln(aα)]/(α–β)]
x = [bβ/aα]1/(α-β)
Здесь x расстояние от начала криволинейного участка до экстремума.
Подставляем это значение в исходное уравнение и определяем y - высоту криволинейного сегмента h. Обозначим параметром γ = [ln(bβ)–ln(aα)]/(α–β)] Тогда: x = eγ и h = aeγα - beγβ
Параметры a, b, α, β нетрудно получить, составив простейшую программу для компьютера на алгоритмическом языке.
сентябрь – ноябрь 2020 г. Вениамин Маркуц
скачать можно здесь
